Research Spotlight: Averaged Invariants in Storage Rings with Synchrotron Motion
When we design a storage ring particle accelerator, we start from certain basic assumptions that are relaxed as we make progress in the design.
We begin by looking at the betatron motion—the horizontal and vertical oscillations that arise from alternating gradient strong focusing. This motion will tell us whether we can stably store a beam. We also look at synchrotron motion—the longitudinal oscillations of the particles in the beam because of time-of-flight dependence on energy and the radiofrequency cavities that accelerate the particles. One of the assumptions we start with is that the betatron and synchrotron motion is independent, or that they are uncoupled.
The benefit of assuming that they are uncoupled is that it allows us to start with three one-dimensional problems instead of one three-dimensional problem. However, they aren’t actually uncoupled. Betatron motion can be linearly coupled in, for example, circular optics or modified with nonlinear dynamics, such as with nonlinear integrable optics. Chromaticity—the dependence of the betatron frequency on the particle’s energy—also can couple the synchrotron motion with the betatron motion, so-called synchro-betatron coupling. This is a coupled nonlinear system that can lead to chaotic dynamics, emittance growth, and other bad things affecting the quality and lifetime of the beam.
Averaged Hamiltonians and Toy Models
Spurred by RadiaSoft’s collaboration on the FAST/IOTA project at Fermilab, we looked into if some sort of general statement can be made about the synchro-betatron coupling.
When we study the long-term dynamics in a storage ring, like the IOTA ring, we want to study the single-turn map. The single-turn map tells us, given some initial position of a particle, what its final position will be after going through the ring once. It turns out, the single-turn map contains all the dynamics of the accelerator, and analyzing it will let us make long-term predictions about the behavior of a beam of particles.
The dynamics of particles around a storage ring are described by a Hamiltonian which generates the single-turn map. This can get deep into the world of symplectic maps and Lie algebras, but the big picture idea is that if we can understand the dynamics of that Hamiltonian, we can understand the dynamics of the particles in the ring, whether the trajectories are stable or not, and so on.
To do this, RadiaSoft scientists first computed an analytic model to predict an averaged Hamiltonian for a particle accelerator ring. The theoretical calculation is high-level and generic, and in practice is probably tricky to calculate anything concrete for a real accelerator. But it does show that, while we might not be able to compute an averaged Hamiltonian in practice, it at least in principle exists. That existence is enough to suggest various stability properties of the accelerator.
What we found is that, outside of resonance issues that arise from the synchrotron tune being a rational number, we can compute a period-averaged Hamiltonian that tells us something about the average motion of the particles over many synchrotron oscillations. We lose some short-time wobbles and wiggles in the trajectory, but we can say broadly whether the dynamics will be well-behaved or not by looking at this averaged Hamiltonian.
To confirm our computation, we built a toy model of a nonlinear ring with synchrotron motion. This was straightforward to implement in a Jupyter notebook. We used a toy 1D single-turn map Hamiltonian that includes chromaticity, linear focusing, and an octupolar nonlinear term for the transverse dynamics, and a thin RF cavity and linear momentum compaction for the longitudinal dynamics.
So the model includes integrable nonlinear transverse dynamics (but no chaos since the octupole term is included as a constant-focusing term), as well as nonlinear synchrotron motion through a nonlinear RF cavity potential.
While the model may not be perfect for a particle accelerator, it lets us compute something with pen and paper and compare it to the simulations.
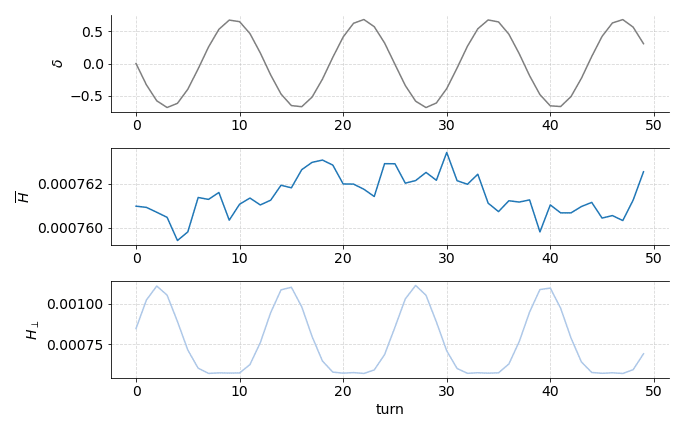
We found that our averaged Hamiltonian is very well-conserved in our toy model with linear synchrotron motion. In this case, we computed the averaged Hamiltonian analytically, because our simple model allowed that.
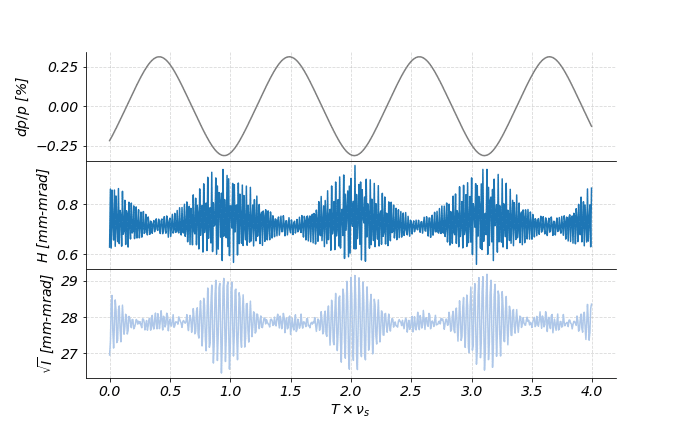
We then compared this averaged Hamiltonian, turn-by-turn, with the unaveraged perpendicular Hamiltonian—that is, the Hamiltonian that contains all the chromatic terms and transverse dynamics, but not the synchrotron motion. What we found is that the perpendicular Hamiltonian has a periodicity with the synchrotron motion, suggesting the existence of some underlying invariant. We also found that the averaged Hamiltonian is very close to invariant over the synchrotron period, suggesting it is that invariant.
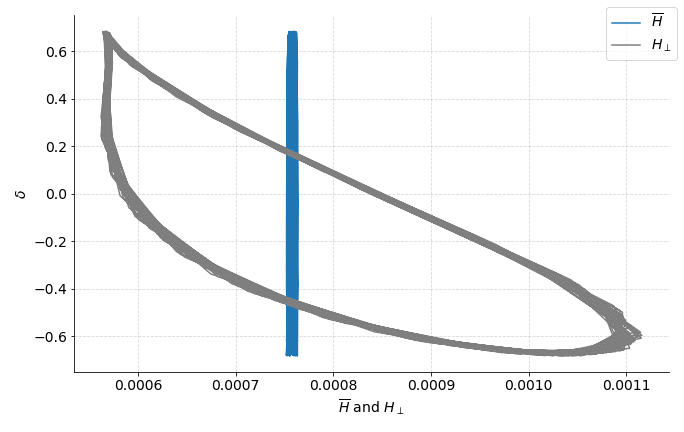
We can also compare this near-conservation to the synchrotron period directly.
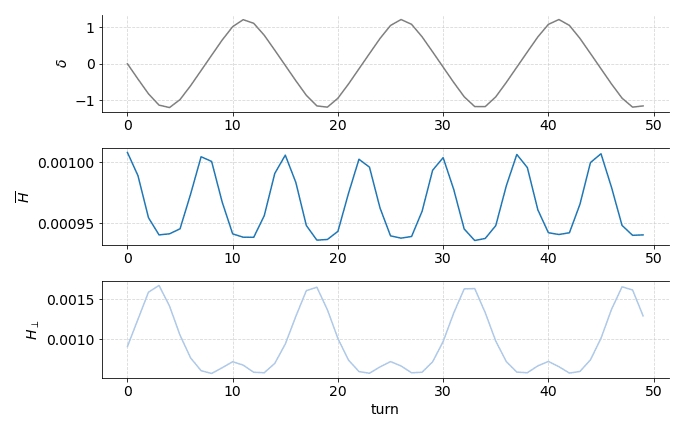
The conservation is in the so-called normal coordinates (see, e.g., É. Forest for a discussion of general linear normal forms) of the linear synchrotron motion, so when we extend to the nonlinear motion we don’t expect conservation since we have not computed the nonlinear normal forms.
In a perturbation theory sense, computing the linear normal forms transforms the linear oscillations to a constant phase advance, so when we look at added nonlinear effects we haven’t canceled out sideband effects and we expect to see oscillations at harmonics of the fundamental. When we add nonlinear synchrotron motion, to account for the curvature in the RF cavity fields, we find oscillations in the invariant commensurate with twice the synchrotron period. This gives us a tell-tale signature that some invariant exists, but we aren’t computing the full normal coordinates, which can be hard to impossible to do effectively for more realistic systems.
Signs of a Hamiltonian in a Real System
Now that we have an intuition for what will happen if we try to apply this reasoning to a complex system, we looked at an integrable Rapid Cycling Synchrotron design developed by Jeff Eldred at Fermilab.
We used Synergia to track the single-particle dynamics, and analyzed the on-momentum invariants for the characteristics we expected from our toy model. Sure enough, we see oscillatory, but bounded, behavior in the invariants that oscillates with the synchrotron period. This bounded behavior suggests there’s an underlying period-averaged Hamiltonian like the one we computed for the toy model, and that the averaged trajectories are integrable, even with the synchrotron motion.

We found a periodic bursting behavior in the non-conservation of the Hamiltonian and second invariant of the lattice as computed in the usual on-momentum linear Twiss coordinates we might be familiar with for computing Courant-Snyder invariants. The periodicity suggests the existence of an underlying invariant, as simply averaging H over the period shows that there is not some spurious drift. The bursting in non-conservation coincides with the particle going from positive to negative energy offset. This corresponds to going to a region where the vertical and horizontal chromaticities are approximately equal, which permits exactly integrable dynamics for off-momentum particles, and a region where the chromaticities are not equal, but this is a subject for another paper.
Conclusion
This computation has strong implications for future nonlinear integrable optics accelerators like the iRCS we studied in this paper. A big concern was what synchro-betatron coupling will do to the integrability of nonlinear integrable optics, and in this paper we offer a mathematical treatment to better understand that question.
Our initial studies suggest that the dynamics will remain regular and well-behaved over long times, and that while we should look out for what synchro-betatron coupling could do, it’s not an immediate show-stopper. It also suggests a path forward for better understanding synchro-betatron coupling in general.