Brightness in Undulators: Challenges & Opportunities

The Importance of Brightness in Undulators

X-ray light sources are a key instrument for scientific discovery in disciplines ranging from biology to materials science to organic chemistry. These light sources are powered by undulators and are used, among other purposes, to examine the ultrafine structures of samples that are under investigation. The ability to measure such fine structures necessitates a high signal-to-noise ratio in the X-ray beam. The beam’s brightness dominates this signal-to-noise ratio, making that brightness a fundamental figure of merit for the undulator. Brightness is such an important feature that the ability to accurately calculate it determines how far beamline designs can advance.

Current and Potential Brightness of Light Sources

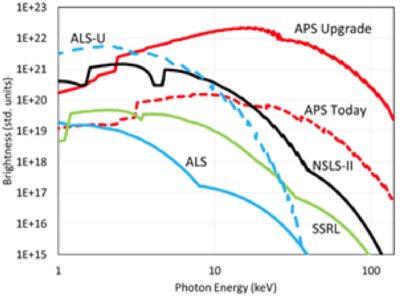
The light sources currently in use show wide variation in brightness and photon energy, with significant improvements anticipated as devices and facilities are updated. Figure 1 (at the top of this article) shows that the brightness of beams produced should increase by two orders of magnitude in the near future. Reaching these hoped-for brightness levels will require overcoming serious difficulties that are rooted in both the beamlines and their sources.

Challenges to Increasing Brightness

One of the challenges to increasing brightness in the beamlines is that their complicated behaviors require high-level mathematics to predict, which in turn requires training and retaining people who can do that work. Brightness calculations require knowing the emitted radiation of the undulator, the photon beam size and divergence, the electron beam energy spread, the photon flux, etc. The math gets twisted pretty fast. Photon flux, for example, is represented by the formula in Figure 2.

Figure 2. Photon Flux Calculations

The components of the photon flux formula are themselves complicated. The formulas for , , , and and are demonstrated in Figure 3.

Figure 3. Additional Calculations

The shifting variables and nested complexity of these mathematical formulas make them difficult to work with or discuss in depth in a blog post. (The references listed at the end of this article provide details for further study). For the purposes of this piece, it’s enough to recognize this barrier to advancement in the field.

Moreover, light sources themselves are enormous and intricate devices; they can cover acres of ground and have thousands of delicate moving parts that require indescribably-minute adjustments in real time. These adjustments must be done by a phalanx of highly-trained engineers and support staff. Suffice to say that any experiment run in such devices is enormously difficult and expensive. Scientists will need to find pathways to lower barriers in both the beamline calculations and the light-source generation in order to continue advancing the field.

Opportunities for Lowering Barriers

The value of high-stakes scientific experiments is, of course, in their complexities. It is neither possible nor desirable to remove them. Lowering barriers to navigating them should be a focus among the community.

The obvious solution is to use software and computational power to handle the calculations and model the behavior of the beamlines and light-source devices. Modeling instead of executing “real” experiments reduces the expense and increases accuracy by orders of magnitude. The sticky bit is that these software programs can be challenging to learn, hard to use, and difficult to share. To truly lower these barriers, another boost is needed. Bringing the simulation codes into a browser or other GUI-based platform can be that boost.

Wrapping the legacy codes in a GUI makes them accessible to scientists and engineers at all stages of their careers. Removing the necessity of learning command-line operations means that any of the multiple codes suitable for X-ray brightness calculations can be used with equal ease. “Drag and drop” inputs make adjustments fast and cheap and multiple iterations easy. GUIs also provide greater visualization capabilities as well as ease of sharing between collaborators.

Using GUI technology to facilitate calculating and modeling tasks is not a silver bullet that removes all barriers. But it is a powerful tool that should be recognized and utilized as scientists seek to achieve the ever-brighter beams that are needed.

Conclusion

Synchrotron radiation production is a hugely important engine for scientific productivity, with applications ranging from basic science to medicine to industry. It is and will continue to be ever-more important to lower barriers both to accurate calculations of brightness and modeling of beamlines in order to advance the development of light sources. Browser-based or GUI technology can lower barriers dramatically and will be an ever-bigger part of the progress in the field of beamline generation. Improving our ability to efficiently quantify the performance of light sources will bring a bright new tomorrow to the light-source community.

References & Resources

The information in this article is drawn from several sources. Please see the references below for further information.

Nash, O.Chubar, N. Goldring, D.L. Bruhwiler, P. Moeller, R. Nagler and M. Rakitin, “Detailed X-ray Brightness Calculations in the Sirepo GUI for SRW,” AIP Conference Proceedings 2054, 060080 (2019); https://doi.org/10.1063/1.5084711

Nash, O.Chubar, D.L. Bruhwiler, M. Rakitin, P. Moeller, R. Nagler, and N. Goldring “Undulator radiation brightness calculations in the Sirepo GUI for SRW,” Proc SPIE 11110, 111100L(2019); http://doi.org/10.1117/12.2530663

M.S. Rakitin, P. Moeller, R. Nagler, B. Nash, D.L. Bruhwiler, D. Smalyuk, M. Zhernenkov and O. Chubar, “Sirepo: an open-source cloud-based software interface for X-ray source and optics simulation,” Journal of Synchrotron Radiation 25, 1877 (2018); https://doi.org/10.1107/S1600577518010986

K.-J. Kim, “Brightness, coherence and propagation characteristics of synchrotron radiation,” NIM A 246, p71 (1986)

This work is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, under Award #DE-SC0011237

Want more RadiaSoft news and content? Sign up for our mailing list.

Research Spotlight: Averaged Invariants in Storage Rings with Synchrotron Motion

When we design a storage ring particle accelerator, we start from certain basic assumptions that are relaxed as we make progress in the design.

We begin by looking at the betatron motion—the horizontal and vertical oscillations that arise from alternating gradient strong focusing. This motion will tell us whether we can stably store a beam. We also look at synchrotron motion—the longitudinal oscillations of the particles in the beam because of time-of-flight dependence on energy and the radiofrequency cavities that accelerate the particles. One of the assumptions we start with is that the betatron and synchrotron motion is independent, or that they are uncoupled.

The benefit of assuming that they are uncoupled is that it allows us to start with three one-dimensional problems instead of one three-dimensional problem. However, they aren’t actually uncoupled. Betatron motion can be linearly coupled in, for example, circular optics or modified with nonlinear dynamics, such as with nonlinear integrable optics. Chromaticity—the dependence of the betatron frequency on the particle’s energy—also can couple the synchrotron motion with the betatron motion, so-called synchro-betatron coupling. This is a coupled nonlinear system that can lead to chaotic dynamics, emittance growth, and other bad things affecting the quality and lifetime of the beam.

Averaged Hamiltonians and Toy Models

Spurred by RadiaSoft’s collaboration on the FAST/IOTA project at Fermilab, we looked into if some sort of general statement can be made about the synchro-betatron coupling.

When we study the long-term dynamics in a storage ring, like the IOTA ring, we want to study the single-turn map. The single-turn map tells us, given some initial position of a particle, what its final position will be after going through the ring once. It turns out, the single-turn map contains all the dynamics of the accelerator, and analyzing it will let us make long-term predictions about the behavior of a beam of particles.

The dynamics of particles around a storage ring are described by a Hamiltonian which generates the single-turn map. This can get deep into the world of symplectic maps and Lie algebras, but the big picture idea is that if we can understand the dynamics of that Hamiltonian, we can understand the dynamics of the particles in the ring, whether the trajectories are stable or not, and so on.

To do this, RadiaSoft scientists first computed an analytic model to predict an averaged Hamiltonian for a particle accelerator ring. The theoretical calculation is high-level and generic, and in practice is probably tricky to calculate anything concrete for a real accelerator. But it does show that, while we might not be able to compute an averaged Hamiltonian in practice, it at least in principle exists. That existence is enough to suggest various stability properties of the accelerator.

What we found is that, outside of resonance issues that arise from the synchrotron tune being a rational number, we can compute a period-averaged Hamiltonian that tells us something about the average motion of the particles over many synchrotron oscillations. We lose some short-time wobbles and wiggles in the trajectory, but we can say broadly whether the dynamics will be well-behaved or not by looking at this averaged Hamiltonian.

To confirm our computation, we built a toy model of a nonlinear ring with synchrotron motion. This was straightforward to implement in a Jupyter notebook. We used a toy 1D single-turn map Hamiltonian that includes chromaticity, linear focusing, and an octupolar nonlinear term for the transverse dynamics, and a thin RF cavity and linear momentum compaction for the longitudinal dynamics.

So the model includes integrable nonlinear transverse dynamics (but no chaos since the octupole term is included as a constant-focusing term), as well as nonlinear synchrotron motion through a nonlinear RF cavity potential.

While the model may not be perfect for a particle accelerator, it lets us compute something with pen and paper and compare it to the simulations.

We found that our averaged Hamiltonian is very well-conserved in our toy model with linear synchrotron motion. In this case, we computed the averaged Hamiltonian analytically, because our simple model allowed that.

We then compared this averaged Hamiltonian, turn-by-turn, with the unaveraged perpendicular Hamiltonian—that is, the Hamiltonian that contains all the chromatic terms and transverse dynamics, but not the synchrotron motion. What we found is that the perpendicular Hamiltonian has a periodicity with the synchrotron motion, suggesting the existence of some underlying invariant. We also found that the averaged Hamiltonian is very close to invariant over the synchrotron period, suggesting it is that invariant.

We can also compare this near-conservation to the synchrotron period directly.

The conservation is in the so-called normal coordinates (see, e.g., É. Forest for a discussion of general linear normal forms) of the linear synchrotron motion, so when we extend to the nonlinear motion we don’t expect conservation since we have not computed the nonlinear normal forms.

In a perturbation theory sense, computing the linear normal forms transforms the linear oscillations to a constant phase advance, so when we look at added nonlinear effects we haven’t canceled out sideband effects and we expect to see oscillations at harmonics of the fundamental. When we add nonlinear synchrotron motion, to account for the curvature in the RF cavity fields, we find oscillations in the invariant commensurate with twice the synchrotron period. This gives us a tell-tale signature that some invariant exists, but we aren’t computing the full normal coordinates, which can be hard to impossible to do effectively for more realistic systems.

Signs of a Hamiltonian in a Real System

Now that we have an intuition for what will happen if we try to apply this reasoning to a complex system, we looked at an integrable Rapid Cycling Synchrotron design developed by Jeff Eldred at Fermilab.

We used Synergia to track the single-particle dynamics, and analyzed the on-momentum invariants for the characteristics we expected from our toy model. Sure enough, we see oscillatory, but bounded, behavior in the invariants that oscillates with the synchrotron period. This bounded behavior suggests there’s an underlying period-averaged Hamiltonian like the one we computed for the toy model, and that the averaged trajectories are integrable, even with the synchrotron motion.

We found a periodic bursting behavior in the non-conservation of the Hamiltonian and second invariant of the lattice as computed in the usual on-momentum linear Twiss coordinates we might be familiar with for computing Courant-Snyder invariants. The periodicity suggests the existence of an underlying invariant, as simply averaging H over the period shows that there is not some spurious drift. The bursting in non-conservation coincides with the particle going from positive to negative energy offset. This corresponds to going to a region where the vertical and horizontal chromaticities are approximately equal, which permits exactly integrable dynamics for off-momentum particles, and a region where the chromaticities are not equal, but this is a subject for another paper.

Conclusion

This computation has strong implications for future nonlinear integrable optics accelerators like the iRCS we studied in this paper. A big concern was what synchro-betatron coupling will do to the integrability of nonlinear integrable optics, and in this paper we offer a mathematical treatment to better understand that question.

Our initial studies suggest that the dynamics will remain regular and well-behaved over long times, and that while we should look out for what synchro-betatron coupling could do, it’s not an immediate show-stopper. It also suggests a path forward for better understanding synchro-betatron coupling in general.

Read the full paper on arXiv here or check out the JINST publication here.

Want more RadiaSoft news and content? Sign up for our mailing list.